Belief-dependent macro-action discovery in pomdps using the value of information
Belief-Dependent Macro-Action Discovery in Pomdps Using the Value of Information
Genevieve Flaspohler, Nicholas Roy, John W Fisher III
Advances in Neural Information Processing Systems 33, 2020.
[pdf] [poster] [slides]

Summary: This work introduces macro-action discovery using value-of-information (VoI) for robust and efficient planning in partially observable Markov decision processes (POMDPs). POMDPs are a powerful framework for planning under uncertainty. Previous approaches have used high-level macro-actions within POMDP policies to reduce planning complexity. However, macro-action design is often heuristic and rarely comes with performance guarantees. Here, we present a method for extracting belief-dependent, variable-length macro-actions directly from a low-level POMDP model. We construct macro-actions by chaining sequences of open-loop actions together when the task-specific value of information (VoI) — the change in expected task performance caused by observations in the current planning iteration — is low. Importantly, we provide performance guarantees on the resulting VoI macro-action policies in the form of bounded regret relative to the optimal policy. In simulated tracking experiments, we achieve higher reward than both closed-loop and hand-coded macro-action baselines, selectively using VoI macro-actions to reduce planning complexity while maintaining near-optimal task performance.

Video Overview



Main Result

This paper introduces a method for generating belief-dependent, variable-length macro-actions using a point-based representation of the POMDP value function. Our key insight is to introduce a value of information (VoI) function — which estimates the change in expected task performance caused by sensing in the current planning iteration — and constrain policies to selectively act open-loop when VoI is low. Unlike hand-coded or learned macro-actions, we show that a horizon- \(H\) policy utilizing VoI macro-actions has bounded regret \(r_h\) compared to the optimal policy. Letting \(V_H^*\) be the expected reward of an optimal policy and \(V_H^{MA}\) the expected reward of the VoI macro-action policy, our main result shows:

\( r_h = \lvert V^*_{H}- V^{MA}_H\rvert_\infty \leq \frac{1-\gamma^H}{1 - \gamma} \left( \delta_{\mathcal{B}} \left(3L + \frac{R_{max}}{1 - k\gamma} + L\gamma k\right)+ \tau \right) \)

where \(\gamma\) is the POMDP discount factor, \(L\) is a Lipschitz constant describing the smoothness of the value function in belief space, and the POMDP reward function is bounded in \([-R_{max}, R_{max}]\).

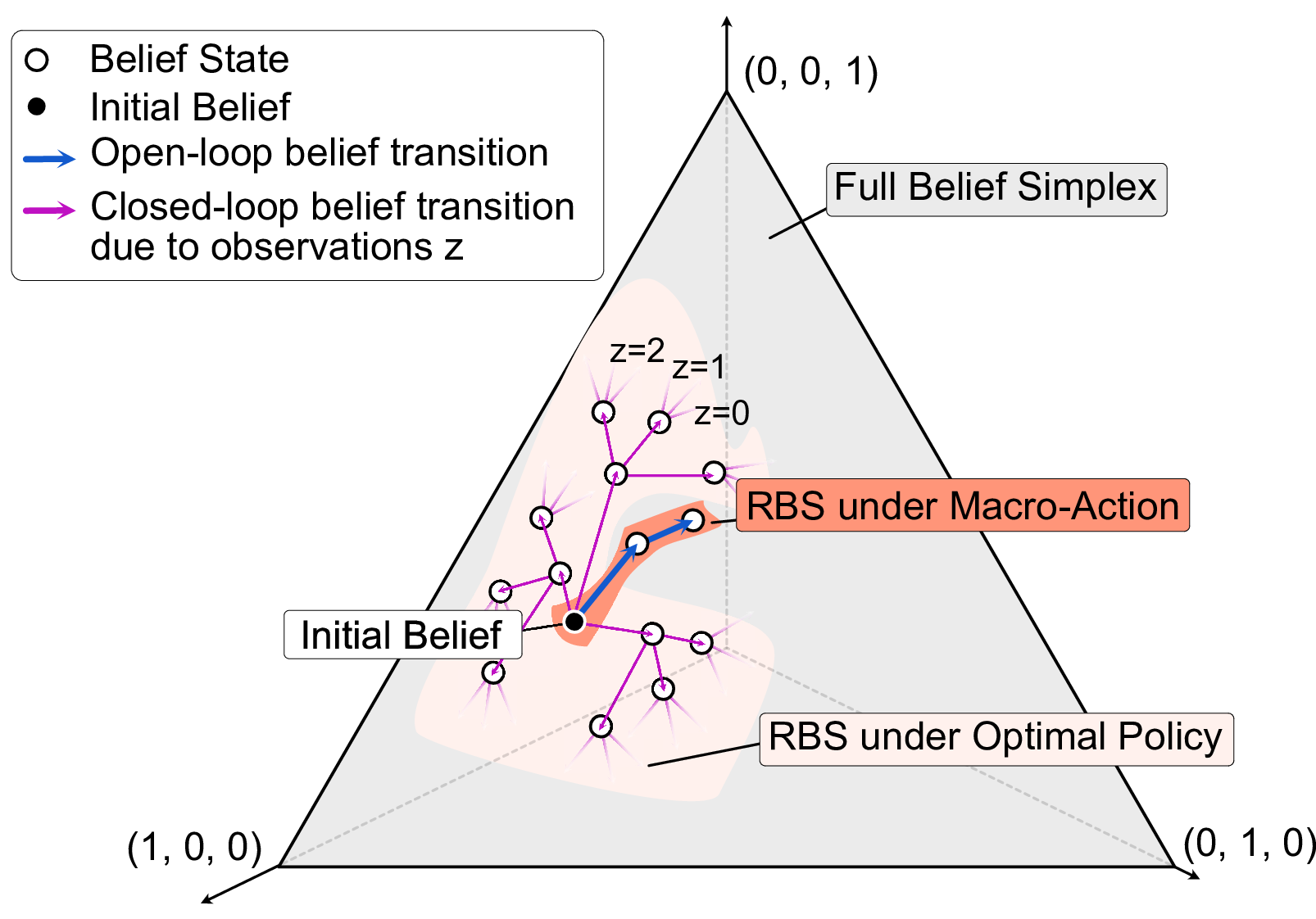
TSP Reachable Belief Space (RBS) and Macro-actions: POMDP planning algorithms often reason over the value of beliefs in a policy's reachable belief space (RBS). However, the size of a policy's RBS generally grows exponentially with the planning horizon in the size of the observation set \(\mathcal{Z}\). This exponential growth is visualized for a three-state discrete POMDP with \(\left|\mathcal{Z}\right| = 3\). Because the belief transitions deterministically under the open-loop VoI macro-actions, the size of the RBS grows only linearly during macro-action execution.