Summary: Articulated motion analysis methods often rely on strong prior knowledge, e.g. as applied to human motion. However, the world contains a variety of articulating objects - mammals, insects, mechanized structures - with parts varying number and configuration. In this paper, we overcome the limitations of traditional methods to learn the properties of novel articulating objects due their reliance on extensive training data ande/or known structures. Our formulation and results include
- A Bayesian nonparametric model of structures with unknown numbers of parts.
- Integration of coupled rigid-body motion dynamics.
- Efficient Gibbs sampling implementation.
- Applicability to differing observation sequence and types.
- No need for markers or learned body models.
Related SLI papers: The work of Straub et al on Manhattan world mixture models (PAMI,CVPR) and Dirichlet process mixture models for spherical data AISTATS.
Video Overview
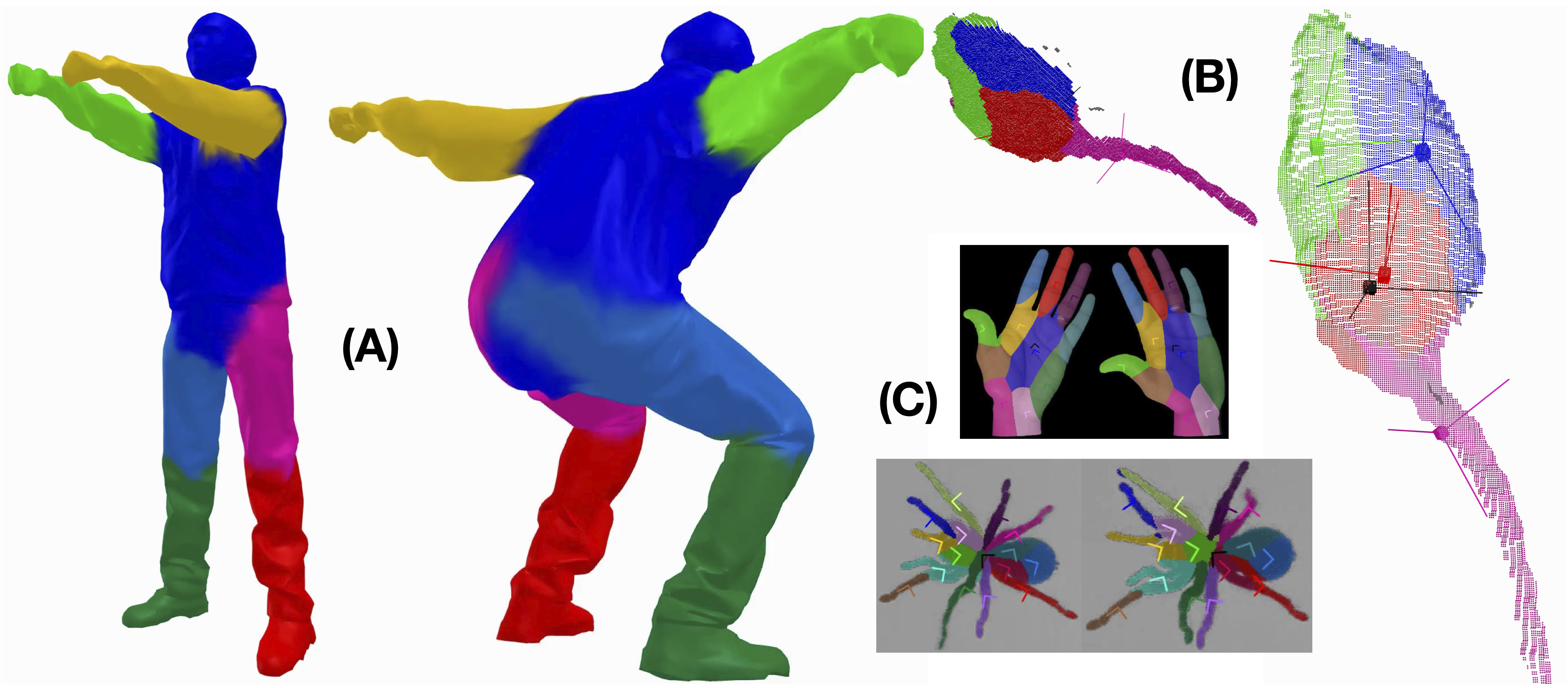
We demonstrate the ability to learn an object’s body/parts decomposition solely from short observation sequences of the object in motion. The model flexibly supports a variety of inputs including 2D pixels, 2.5D RGB-depth, and 3D point clouds/meshes. Parts are modeled as rotating and translating about a body frame of reference, but with a biased random walk so that they never wander too far from a typical, learned location. In this way, we need not impose prior assumptions about part shape or extent, but maintain robust associations of observations to parts.
|
The number, rotation, translation, and shape of an object's parts are learned from a small number of observations of that object in motion. Motion of the body and parts is parameterized by the Lie group of rigid transformations in 3D or 2D. Supported data sources include sequences of meshes / point clouds (A, human), depth data (B, marmoset), and 2D images (C, hand, spider) |
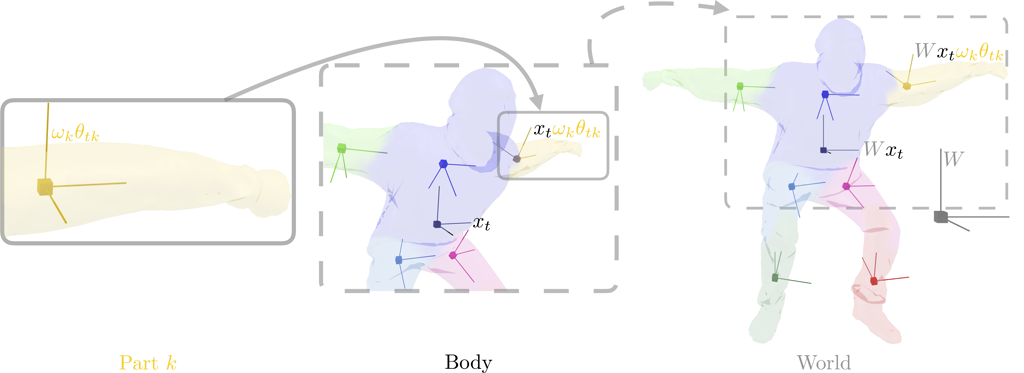
| Objects are decomposed into relative coordinate frames going from world to body to part. Relations are defined by rigid-body transformations that vary dynamically with time. Parts remain "close" to a (relative) central location via stabilized random walk. |
|
Some cool videos or figures.
Perhaps an Overview video
