Summary: In many sequential planning applications a natural approach to generating high quality plans is to maximize an information reward such as mutual information (MI). Unfortunately, MI lacks a closed form in all but trivial models, and so must be estimated. In applications where the cost of plan execution is expensive, one desires planning estimates which admit theoretical guarantees. Through the use of robust M-estimators we obtain bounds on absolute deviation of estimated MI. Moreover, we propose a sequential algorithm which integrates inference and planning by maximally reusing particles in each stage. We validate the utility of using robust estimators in the sequential approach on a Gaussian Markov Random Field wherein information measures have a closed form. Lastly, we demonstrate the benefits of our integrated approach in the context of sequential experiment design for inferring causal regulatory networks from gene expression levels. Our method shows improvements over a recent method which selects intervention experiments based on the same MI objective. In our analysis we:

• formulate the estimator bias,
• establish a central limit theorem and consistency,
• show probabilistic bounds of estimator deviation for finite samples,
• and present a probabilistic statement of plan quality.

Related SLI papers: The work of Ertin et al formulating MI in dynamic sensor query problems Ertin 2003, Williams et al formulating information-driven sensor planning as constrained optimization Williams 2007, and Siracusa et al on Bayesian structure inference Siracusa 2009.

We derive a sequential algorithm is motivated by sequential importance sampling (IS) for static models introduced by Chopin 2002; a special case of resample-and-move for dynamical systems (Gilks & Berzuini 2001). Drovandi et al. 2014 propose a similar approach for experimental design in model selection, though they only consider discrete observations and rely on the standard IS estimate of the model evidence. It requires \(N\) posterior samples at each stage \(t\) and for each action \(1,…,A\) an additional \(M\) posterior samples are needed. Sample complexity is thus \(O\left(TNAM\right)\). As a practical alternative we propose a sequential importance sampling approach that encourages sample reuse thereby reducing computation.

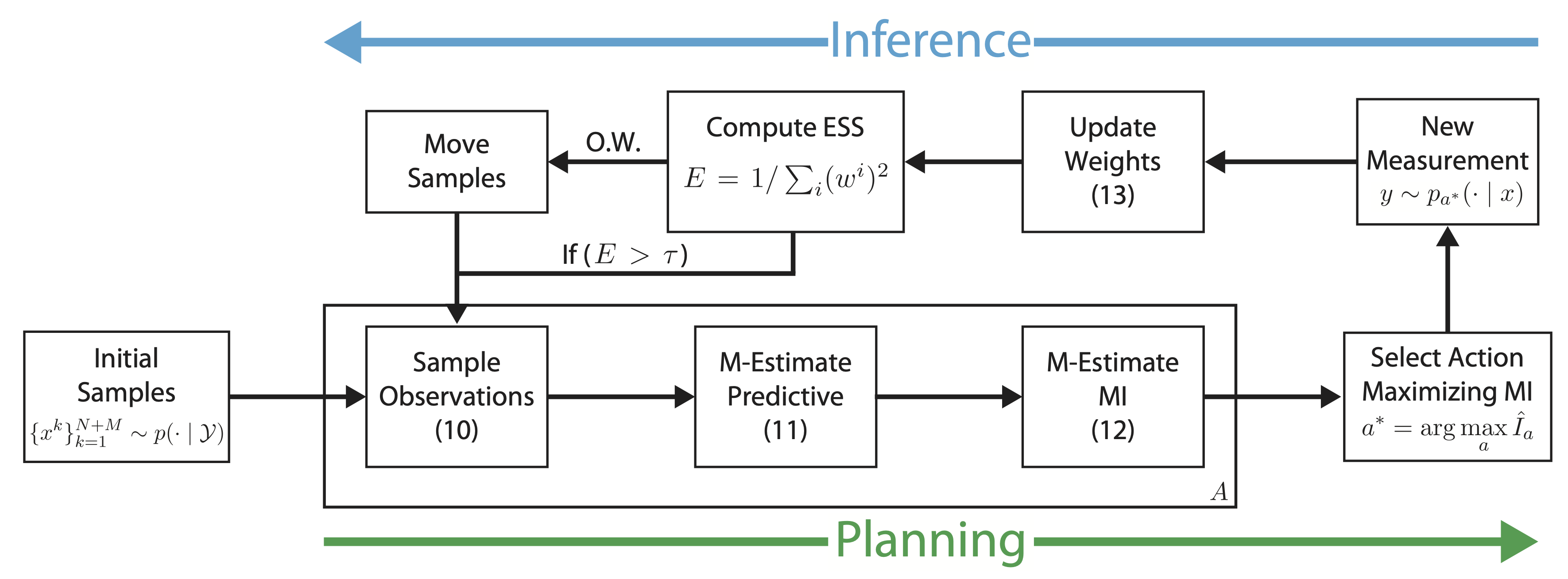
Sequential Algorithm: Our algorithm performs closed-loop greedy planning by alternating inference and planning stages. Planning: samples \(y^i \sim p_a\) are drawn for each potential action \(a = 1, ... , A\), followed by robust importance-weighted MI estimates. Note that planning estimates can be computed in parallel for all actions. Inference: After selecting action \(a^∗ = \arg \max_{a} \hat{I}_a\) an observation is drawn from the corresponding model \(y \sim p_{a^∗}\left(y | x\right)\). Importance weights are then updated and new posterior samples are drawn if the effective sample size (ESS) drops below the threshold \(\tau\) . Numbers reference corresponding equations in the main text.

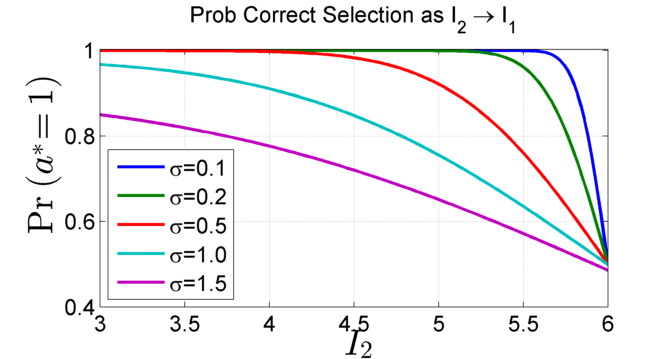
Estimator Quality versus Correct Selection: The method relies on the use of a robust estimator. The figure below show that as the ability to determine the precise ordering of information rewards for each action decreases, so does the regret, i.e., the difference in the reward as a consequence of making an incorrect choice.

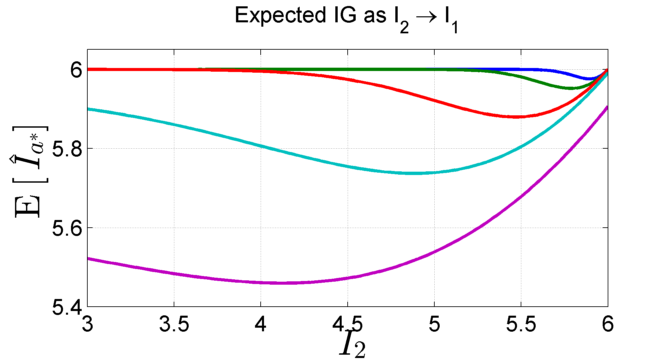
Left: Probability of correct ranking: We vary \(I_2\) from \(I_3\) to \(I_1\) where \(I_1, I_3, I_4, I_5 = 6, 3, 2, 1\) respectively. As \(I_2\) approaches \(I_1\), the probability of selecting the correct optimizer \(\mathbb{P}(a^* =1)\), which depends on \(\left(I_1 - I_2\right)/\sigma\), drops as there is increasing chance of selecting \(a^* = 2\). Right: Expected information gain: While the probability of selecting the correct maximizer decreases as \(I_2 \rightarrow I_1\), these actions have increasingly similar IG and the net reduction in expected IG for choosing the incorrect optimizer is small.

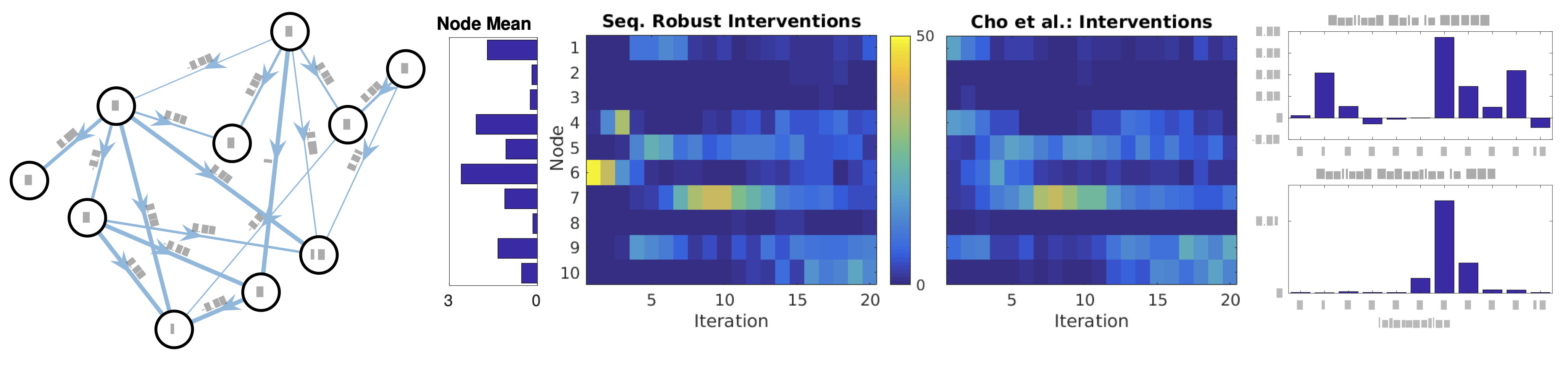
Application to Causal Gene Regulatory Networks: Here the goal is to plan a sequence of so-called knock out experiments (i.e., interventions) in order to discover causal relations between expressed genes.

Regulatory network planning: The true network structure shows edges labeled by weights \(w_{ij}\) (left). The magnitude of the node mean in true network in the absence of any intervention (center-left) correlates strongly with selection sequence by Robust (center) since zeroing the expression level of a highly expressive gene is expected to induce large changes. Interventions chosen under Robust and Cho et al (center-right) from 50 trials. At early iterations Robust selects interventions consistently across trials whereas Cho et al’s method exhibits greater variability in the selection process. In both, greater variance is seen at later iterations when the optimal choice diverges across trials due to differences in selection history and in realized observations. The average performance gain realized after performing the specified intervention at \(t = 1\) (right) indicates that clamping node 6 is by far the optimal choice.