Summary: Mutual information (MI) is a commonly adopted utility function in Bayesian optimal experimental design [see Blackwell 1950, Lindley 1956 & Bernardo 1979]. While theoretically appealing, MI evaluation poses a significant computational burden for most real world applications. As a result, many algorithms utilize MI bounds as proxies that lack regret-style guarantees. Here, we utilize two-sided bounds to provide such guarantees. Bounds are successively refined/tightened through additional computation until a desired guarantee is achieved. We consider the problem of adaptively allocating computational resources in BOED. Our approach achieves the same guarantee as existing methods, but with fewer evaluations of the costly MI reward. We adapt knapsack optimization of best arm identification problems, with important differences that impact overall algorithm design and performance. First, observations of MI rewards are biased. Second, evaluating experiments incurs shared costs amongst all experiments (posterior sampling) in addition to per experiment costs that may vary with increasing evaluation. We propose and demonstrate an algorithm that accounts for these variable costs in the refinement decision. Specifically, we

• incorporate both lower and upper bounds on the intractable MI utility into BOED to provide performance guarantees relative to the optimal design and show how they can be maintained with minimal additional computation,
• introduce a cost-sensitive sequential optimization that iteratively refines bounds to target a desired performance level,
• formulate a greedy knapsack optimization that elegantly trades off performance for computation, and
• evaluate our BOED method against adaptive allocation techniques in Gaussian models as well as the challenging problem of multi-target tracking.

Related SLI papers: Williams formulates information gathering in distributed networks in Williams et al 2007 as a Markov Decision Process subject to resource constraints and subsequently develops theoretical guarantees on MI based sensor selection Williams at al 2007 (AIStats). Zheng develops MCMC-based information planning Zheng et al algorithms along with analysis of estimator deviation bounds. Pacheco develops a variational formulation of information planning including bounds on the variational approximation of the information reward in Pacheco et al.

Video Overview

The approach makes use of two Monte Carlo estimators of MI: $$\mathit{l} = \frac{1}{N} \sum_{n=1}^N \log \frac{p(y_n | x_n)}{\frac{1}{N} \sum_{m=1}^N p(y_n | x_m)}, \quad \mathit{u} = \frac{1}{N} \sum_{n=1}^N \log \frac{p(y_n | x_n)}{\frac{1}{N-1} \sum_{m \neq n} p(y_n | x_m)}$$ and the fact that they are (in expectation) lower and upper bounds Foster 2019 and 2020 $$\mathbb{E} \left[\mathit{l} \right] \leq I\left(X;Y\right) \leq \mathbb{E}\left[\mathit{u}\right]$$

Algorithms

The standard BOED algorithm is shown above where a sample-based estimator is used as a proxy for the MI reward. In contrast, the variable cost structure algorithm below incorporates sample-based bounds on MI combined with an iterative refinement scheme that yields reduced computation and performance guarantees. Equation numbers correspond to the published paper.

Experimental Result

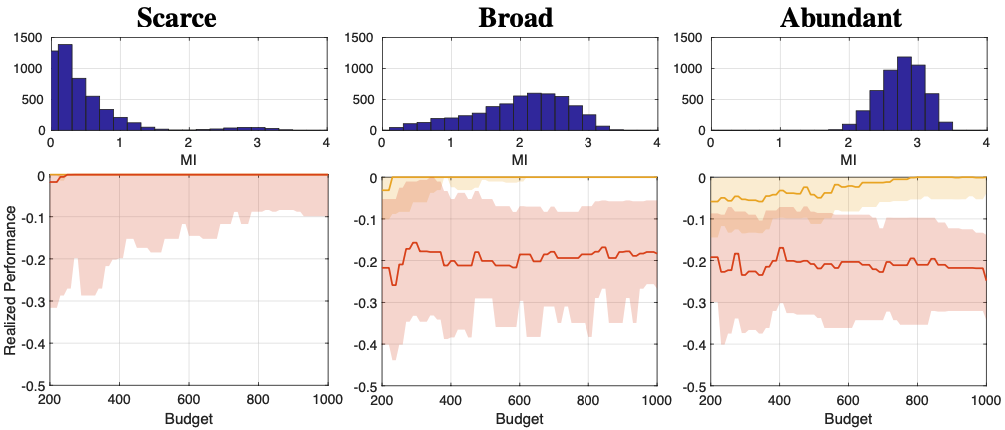
Realized Performance Across Motifs in BOED. Top-row: Three distributions over MI rewards characterize different problem structures or ``motifs''. Bottom-row: Median and quartiles performance (information gain relative to optimal) under proxy-based BOED framework for two proxies under various budgets: lower bound (bed-lb) and upper bound (bed-ub). Motifs are: scarce mostly uninformative (left), broad similarly informative (middle), and abundant mostly informative (right). Performance varies greatly depending on the proxy used and the problem structure, leading to wasted compute cycles when the specified budget is too large (scarce with bed-lb) or poor performance when not large enough (abundant with bed-ub).